jochen.rethmann(at)hsnr.de
Letzte Änderung: 23.06.2025
Industrielle Abstapelanlagen, sogenannte Palettierer, werden in verschiedenen Branchen eingesetzt und von verschiedenen Herstellern angeboten. Bei Endverpackungssystemen werden unterschiedlich große Behälter, oft sind es Kartons, durch einen Palettierroboter zum Transport auf eine Palette gestapelt. Dabei sind die Kartons so auf die Paletten zu stapeln, dass möglichst wenige Paletten benötigt werden, also viele Kartons auf eine Palette passen, die Lücken zwischen den Kartons also klein sind. Das zu lösende, zugrundeliegende Problem ist das dreidimensionale Bin-Packing-Problem.
Bei Filialsystemen werden dagegen oft gleich große, stabile, wiederverwendbare Behälter verwendet. Solche Systeme finden wir im Buchhandel, bei Apotheken oder auch bei Warenhäusern. Die Anordnung der Behälter auf der Palette wird nur einmal berechnet und kann daher als bekannt vorausgesetzt werden. Hier ist das Problem, die Paletten so zu stapeln, dass beim Ausliefern der Ware in einer Tour das Entladen des LKW möglichst einfach ist, also möglichst wenig umgestapelt werden muss. Das Abstapeln ist also abhängig von den Bestellungen der einzelnen Filialen.
Oft werden die Filialen großer Warenhäuser von einem Zentrallager aus mit Waren beliefert. Die Artikel werden zum Versand in stabile, wiederverwendbare, gleich große Behälter verpackt, die gefüllten Behälter werden anschließend in einer Abstapelanlage auf Paletten gestapelt. Jede Palette enthält nur Behälter einer einzigen Filiale, damit bei der Auslieferung per LKW kein Umsortieren nötig ist.

Die zu stapelnden Behälter werden in der Regel auf einem Transportband bei der Abstapelanlage angeliefert. Dort werden die Behälter auf ein zyklisches Transportband geleitet. Von diesem zyklischen Transportband werden die Behälter auf Pufferbänder ausgeschleust, an deren Enden die Behälter von automatischen Greifarmen aufgenommen und auf die direkt dahinter befindliche Palette gestapelt werden. Eine vollständig beladene Palette wird automatisch abtransportiert und durch eine leere Palette ersetzt. Das zyklische Transportband kann auch als Speicher für Behälter genutzt werden, indem die Behälter mehrere Runden auf dem Transportband verbleiben.
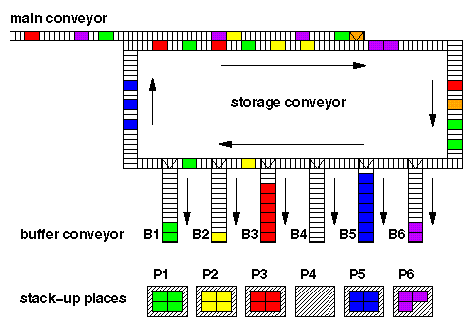
Die Firma Bertelsmann betreibt eine Abstapelanlage mit 24 Stapelplätzen und einem zyklischen Speicher, der circa 60 Behälter aufnehmen kann. An einem einzigen Tag werden damit mehrere tausend Behälter abgestapelt. Die Abbildung 1 skizziert eine solche Anlage. Alle Behälter einer Farbe sind für die gleiche Filiale bestimmt. Allein in Deutschland gibt es über 90 Filialen des Club Centers, die vom Zentrallager aus beliefert werden. Die Bestellung einer Filiale kann mehrere Paletten umfassen, so dass man von mehreren hundert Paletten ausgehen kann, die pro Tag gestapelt werden.
zurück zur Startseite
In industriellen Abstapelanlagen sind die Pufferbänder und der zyklische Speicher technisch bedingt nötig, da zum Beispiel die Greifarme in der Regel nur ruhende Behälter aufnehmen können. Zur Bestimmung der Reihenfolge, in der die Behälter zu Paletten abgestapelt werden, sind solche Details jedoch nicht notwendig. Wir beschreiben die realen Anlagen mit zwei unterschiedlichen Modellen, die sich darin unterscheiden, wie die Behälter zwischengespeichert werden und wie auf die Behälter zugegriffen werden kann.
Wir nennen eine Abstapelanlage blockiert, wenn alle Stapelplätze durch Paletten belegt sind und (im Speicher) auf keinen Behälter zugegriffen werden kann, der für eine auf den Stapelplätzen befindliche Palette bestimmt ist. In einem solchen Fall müssen einige Behälter von Hand abgestapelt werden, was zusätzliche Kosten verursacht und daher verhindert werden soll. Soweit uns bekannt ist, beruhen die Steuerungsalgorithmen der Abstapelanlagen auf Fuzzy-Logik Ansätzen. Unsere Modelle ermöglichen erstmals die Entwicklung effizienter, diskreter Algorithmen zur beweisbar guten Steuerung von Abstapelanlagen.
Um die Komlexität des Problems sowie die Laufzeiten und Güte der von uns entwickelten Algorithmen angeben zu können, verwenden wir folgende Bezeichnungen:
Der Zustand, in dem sich die Anlage befindet, wird eindeutig beschrieben durch die Belegung des Speichers mit Behältern, den bereits vollständig abgearbeiteten Paletten und den aktuell auf den Paletten gestapelten Behältern. Einen solchen Zustand nennen wir Konfiguration.
In diesem Modell fassen wir den zyklischen Speicher und die Pufferbänder zu einem Speicher mit wahlfreiem Zugriff zusammen. Die Abbildung 2 zeigt dieses vereinfachte Modell einer Abstapelanlage. In der realen Anlage können auf jedem Pufferband etwa 10 Behälter, und auf dem zyklischen Transportband ungefähr 60 Behälter gespeichert werden. Bei 24 Pufferbändern ergibt sich also eine Speicherkapazität von circa 300 Behältern.
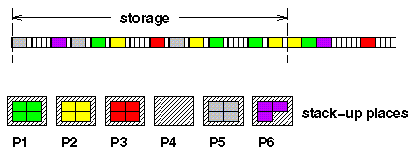
Aus theoretischer Sicht betrachten wir das Abstapelproblem folgendermaßen. Gegeben ist eine Abstapelanlage mit p Stapelplätzen und einem Speicher, der s Behälter aufnehmen kann, sowie eine Sequenz paarweise verschiedener Behälter. Jeder dieser Behälter ist genau einer Palette zugeordnet. Der Speicher enthält zu Beginn die ersten s Behälter der Sequenz. Wird ein Behälter aus dem Speicher entfernt, so rücken alle Behälter rechts davon um eine Position nach links auf und der erste Behälter der Restsequenz rückt in den Speicher nach.
Das (Entscheidungs-) Problem besteht darin, die Behälter nacheinander aus dem Speicher zu entfernen, so dass während der Abarbeitung maximal p Stapelplätze benutzt werden. Bei dem (Optimierungs-) Problem wird entweder die Speicherkapazität s oder die Anzahl der Stapelplätze p vorgegeben, und eine Abarbeitung der Sequenz gesucht, bei der der jeweils andere Parameter minimiert wird.
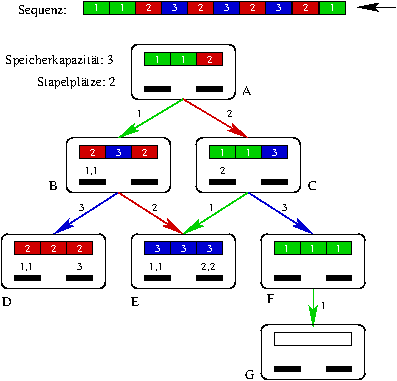
In Abbildung 3 betrachten wir ein Beispiel: Die Sequenz besteht aus zehn Behältern, die für insgesamt drei Paletten bestimmt sind. Initial befinden sich die ersten drei Behälter der Sequenz im Speicher, die Stapelplätze sind leer. In diesem initialen Zustand A kann im nächsten Schritt ein Behälter, der Palette 1 (grün) zugeordnet ist, oder ein Behälter, der Palette 2 (rot) zugeordnet ist, aus dem Speicher entfernt werden. Diese Wahlmöglichkeiten sind in der Abbildung mit den Pfeilen dargestellt.
Betrachten wir zunächst den Fall, dass ein (grüner) Behälter für Palette 1 aus dem Speicher entfernt wird. Dann rückt der erste (blaue) Behälter für Palette 3 nach. Es befindet sich dann aber immer noch ein (grüner) Behälter für Palette 1 im Speicher, der ebenfalls entfernt werden kann. Dann rückt der zweite (rote) Behälter für Palette 2 in den Speicher nach. Dieser Zustand wird durch Konfiguration B dargestellt. In dieser Konfiguration können wir die (roten) oder die (blauen) Behälter für Paletten 2 oder 3 aus dem Speicher entfernen. Wenn wir die Behälter in der Reihenfolge (1,2,3,5,7) entfernen, dann erreichen wir den Zustand E, bei dem beide Stapelplätze belegt sind, die letzten Behälter für die entsprechenden Paletten noch nicht in den Speicher transportiert werden konnten, und alle im Speicher befindlichen Behälter nicht für die auf den Stapelplätzen bereitstehenden Paletten bestimmt sind: Es wurde eine blockierende Konfiguration erreicht.
Betrachten wir nun den Fall, dass wir in der initialen Konfiguration den (roten) Behälter für Palette 2 aus dem Speicher entfernen. Dann rückt der (blaue) Behälter für Palette 3 nach. Dieser Zustand wird durch Konfiguration C dargestellt. Wird dieser (blaue) Behälter für Palette 3 ebenfalls entfernt, dann können nacheinander alle roten und blauen Behälter entfernt werden, so dass anschließend beide Stapelplätze frei werden. Die Abarbeitung erreicht so Konfiguration F. Zum Schluss können dann die grünen Behälter abgestapelt werden. Die Reihenfolge, in der die Behälter bei dieser Lösung abgestapelt werden, ist (3,4,5,6,7,8,9,1,2,10). Eine solche Reihenfolge nennen wir Behälterlösung. Die Reihenfolge (2,3,1) nennen wir Palettenlösung: Wird zum ersten Mal ein Behälter für eine Palette aus dem Speicher entfernt, dann notieren wir diese Palette. In unserem Beispiel wird im ersten Schritt ein Behälter für die Palette 2 entfernt, im nächsten Schritt ein Behälter für die Palette 3, und im Schritt 8 zum ersten Mal ein Behälter für die Palette 1. Eine solche Palettenlösung ist ausreichend, um eine Reihenfolge zu bestimmen, in der die Behälter abgestapelt werden können.
Eine Sequenz, die mit einer Speicherkapazität von s Behältern und mit p Stapelplätzen abgearbeitet werden kann, nennen wir (s,p)-Sequenz; eine solche Abarbeitung nennen wir entsprechend eine (s,p)-Abarbeitung. Uns sind weder Komplexitätsanalysen, algorithmische Lösungsansätze noch ähnliche Problemstellungen aus der Literatur von anderen Autoren bekannt.
Wir konnten mittels einer Reduktion auf das SAT-Problem zeigen, dass das Abstapelproblem im allgemeinen Fall NP-vollständig ist. Das Problem kann aber in polynomieller Zeit gelöst werden, wenn die Kapazität des Speichers s oder die Anzahl der Stapelplätze p konstant ist. Allerdings bleibt das Problem NP-vollständig, selbst wenn die Sequenzen nur bis zu 9 Behälter pro Palette enthalten oder die Anzahl der Behälter für alle Paletten gleich ist. Für den Spezialfall, dass jeder Palette höchstens drei Behälter zugeordnet sind, konnten wir einen polynomiell zeitbeschränkten Algorithmus angeben.
muss noch untersucht werden ...
Wir entwickelten einen polynomiell zeitbeschränkten Approximationsalgorithmus, der jede (s,p)-Sequenz mit einer Speicherkapazität von s · log(p+1) Behältern und mit p+1 Stapelplätzen abarbeitet. Ferner konnten wir zeigen, dass unter der Annahme P ungleich NP kein polynomiell zeitbeschränkter Algorithmus existiert, der für jede (s,p)-Sequenz eine (s+c,p+k)-Abarbeitung der Sequenz liefert, wobei c und k zwei konstante natürliche Zahlen sind.
Wir untersuchten das worst-case Verhalten einfacher Algorithmen, die nicht die gesamte Sequenz im voraus kennen, sondern nur die Behälter, die sich augenblicklich im Speicher befinden. Wir konnten zeigen, dass der Most-Frequently Algorithmus (2,2)-competitive ist, d.h. dieser Algorithmus berechnet zu jeder beliebigen (s,p)-Sequenz eine Abarbeitung, für die bei einer Speicherkapazität von 2s Behältern maximal 2p Stapelplätze benötigt werden. Ferner konnten wir zeigen, dass der Most-Frequently Algorithmus im Vergleich zu anderen on-line Algorithmen bzgl. der worst-case Performanz optimal ist.
Das Modell mit wahlfreiem Speicherzugriff war ein erster Versuch, die Abstapelproblematik zu modellieren und wesentliche Einflussgrößen der Systeme auf den Abstapelvorgang zu erfassen. Das folgende Modell mit Pufferbändern scheint die real existierenden Abstapelsysteme besser zu modellieren und die Einflüsse auf den Abstapelvorgang präziser zu erfassen.
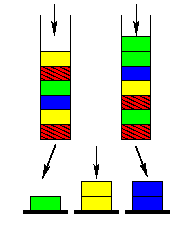
In diesem Modell vernachlässigen wir den zyklischen Speicher, und wir gehen davon aus, dass alle Behälter zu Beginn bereits auf (potenziell unendlich lange) Pufferbänder verteilt sind. Damit das Modell möglichst viele verschiedene, reale Anlagen beschreiben kann, ist die Anzahl der Stapelplätze und die Anzahl der Pufferbänder nicht korreliert, also unabhängig voneinander. Die Robotergreifarme können jeweils den ersten Behälter eines Pufferbandes aufnehmen und auf die Palette eines beliebigen Stapelplatzes ablegen. Die Abbildung 4 zeigt dieses vereinfachte Modell einer Abstapelanlage. Wir wollen im Weiteren vom FIFO-Abstapelproblem sprechen, um es vom obigen Problem zu unterscheiden.
Aus theoretischer Sicht betrachten wir das FIFO-Abstapelproblem folgendermaßen. Gegeben ist eine Abstapelanlage mit p Stapelplätzen und k Pufferbändern. Die Pufferbänder sind zu Beginn bereits mit Behältern gefüllt, und jeder dieser Behälter ist genau einer Palette zugeordnet. Wird ein Behälter von der ersten Position eines Pufferbandes entfernt, so rücken alle Behälter dahinter um eine Position nach vorne auf. Das Problem besteht darin, die Behälter nacheinander aus den Pufferbändern zu entfernen, so dass während der Abarbeitung maximal p Stapelplätze benutzt werden.
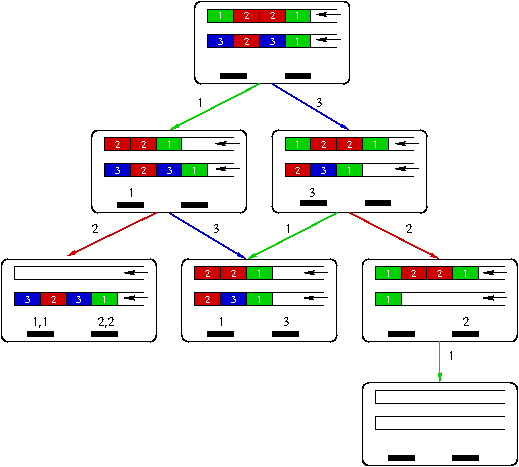
Auch in diesem Modell spielt die Reihenfolge, in der die Behälter abgestapelt werden, eine entscheidende Rolle. In Abbildung 5 sind die Entscheidungen in Form eines Graphen visualisiert. Zu Beginn sind die beiden Stapelplätze leer, die Pufferbänder sind komplett gefüllt. In der initialen Konfiguration kann aus dem ersten Pufferband der (grüne) Behälter für Palette 1 oder aus dem zweiten Pufferband der (blaue) Behälter für Palette 3 entfernt werden. Eine Abarbeitung der Sequenzen ist nur für die Palettenlösung (3,2,1) möglich. Alle anderen Reihenfolgen führen in blockierende Konfigurationen.
In Abbildung 5 sind nur die Konfigurationen gezeigt, in denen eine echte Entscheidung getroffen werden muss: Kann ein Behälter aus einer der Sequenzen entfernt werden, der für eine Palette bestimmt ist, die bereits auf einem Stapelplatz abgestapelt wird, dann dürfen wir diesen Behälter auch entfernen, ohne dass wir einen Fehler machen. So können die Behälter aus der ersten Sequenz automatisch abgestapelt werden, nachdem die beiden ersten Behälter entfernt wurden, siehe linken Zweig der Abbildung 5. Wir betrachten daher in der Abbildung und auch bei unseren Untersuchungen nur sogenannte Entscheidungskonfigurationen.
Die Behälter werden in realen Anlagen auf einem Transportband bei der Abstapelanlage angeliefert. Daher muss zunächst eine Zuordnung der Behälter auf die Pufferbänder erfolgen. In dem hier untersuchten Modell gehen wir davon aus, dass diese Aufteilung bereits erfolgt ist. In einem zweiten Schritt müsste man untersuchen, wie komplex es ist, die Behälter einer einzigen gegebenen Behältersequenz so auf k Pufferbänder aufzuteilen, dass anschließend eine Abarbeitung mit p Stapelplätzen möglich ist.
Zusätzlich zu den allgemeinen Parametern verwenden wir in diesem Modell den Parameter k, um die Anzahl der Sequenzen zu beschreiben. In der uns bekannten realen Abstapelanlage gibt es 24 Pufferbänder.
Wir konnten mittels einer Reduktion auf das Wegweite-Problem zeigen, dass das FIFO-Abstapelproblem im Allgemeinen NP-vollständig ist. Das Problem bleibt NP-vollständig selbst für solche Sequenzen, die maximal sechs Behälter pro Palette enthalten.
Wir definieren zu einer Liste Q von Behälter-Sequenzen den gerichteten Graphen GQ, dessen Knotenmenge die Paletten repräsentiert, und der eine gerichtete Kante von Palette a zu Palette b enthält, wenn es eine Sequenz gibt, in der ein Behälter der Palette a links von einem Behälter der Palette b enthalten ist. Die Sequenzen können genau dann mit p Stapelplätzen abgearbeitet werden, wenn der Graph GQ eine gerichtete Wegweite von höchstens p-1 hat. Da Bounded Directed Pathwidth in polynomieller Zeit berechnet werden kann, ist auch das FIFO-Abstapelproblem in polynomieller Zeit lösbar, wenn die Anzahl p der Stapelplätze konstant ist.
Gibt es nur konstant viele Sequenzen, ist also k konstant, dann kann ebenfalls in polynomieller Zeit eine Lösung berechnet werden.
Es kann maximal m! viele verschiedene Reihenfolgen geben, in denen die Paletten aufgezählt werden. Jede dieser Reihenfolgen kann in Zeit O(n2) daraufhin getestet werden, ob diese Reihenfolge eine Abarbeitung mit maximal p Stapelplätzen ermöglicht. Also kann in Zeit O(n2 · m!) das FIFO-Abstapelproblem gelöst werden. Das FIFO-Abstapelproblem ist also fpt bezogen auf die Anzahl der Paletten m.
Viele dieser Paletten-Reihenfolgen können aber nicht in eine Behälterlösung umgewandelt werden und stellen daher keine Lösung des Problems dar. Im obigen Beispiel in Abbildung 5 kann im ersten Schritt kein (roter) Behälter der Palette 2 aus dem Speicher entfernt werden. Also stellen alle Paletten-Reihenfolgen, die mit (2, …) beginnen, keine Lösung dar. Zu einer Abarbeitung der Sequenzen definieren wir die Folge L = (l1, l2, …, lm), wobei der Wert li die Sequenz angibt, dessen erster Behälter in der i-ten Entscheidungskonfiguration entfernt wird. Es gibt maximal O(km) viele solcher Reihenfolgen. Jede dieser Reihenfolgen kann in Zeit O(n2) daraufhin getestet werden, ob diese Reihenfolge eine Abarbeitung mit maximal p Stapelplätzen ermöglicht. Also kann in Zeit O(n2 · km) das FIFO-Abstapelproblem gelöst werden. Da k in der Praxis viel kleiner als m ist, ist diese Laufzeit deutlich besser als O(n2 · m!).
Das FIFO-Abstapelproblem kann mit einem Fehler von höchstens O(log1,5(m)) approximiert werden. Diese Aussage basiert auf der Darstellung des Problems mittels des Graphen GQ. Approximationsalgorithmen für das Problem der gerichteten Wegweite können daher genutzt werden, um auch für das FIFO-Abstapelproblem eine Approximation zu erhalten.
muss weiter untersucht werden ...
zurück zur Startseite